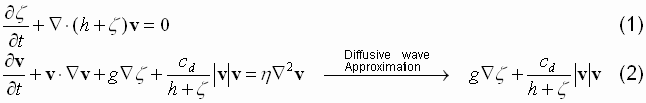
Estuarine Hydrodynamic Equations
The shallow water equations (2D, depth averaged) accurately capture estuarine hydrodynamics. Although the full equations can be solved,
Ip et al. have shown that a kinematic approximation to these equations can be employed in shallow estuaries, which reduces computational overhead. We have adopted Ip et al.'s approach, which we briefly describe here (please see Ip et al. for details). What Ip et al. refer to as a kinematic approximation to the shallow water equations is actually a diffusive wave approximation (cf. Ferrick and Goodman) and is given by: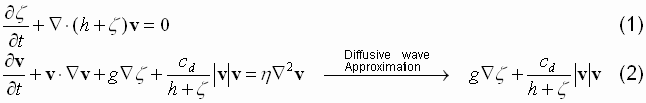
where ![]() is the water surface deviation measured from a datum,
is the water surface deviation measured from a datum,

The kinematic approximation allows the hyperbolic advection eqn. (2) to be converted into a parabolic diffusion eqn. (3), which is numerically easier to solve.

To handle flooding and drying of the marsh without using a moving boundary,
Ip et al. assume there exists a porous sub-layer (figure on right) where water flow, q, follows Darcy's Law:![]()
where ![]() is the hydraulic conductivity and
is the hydraulic conductivity and
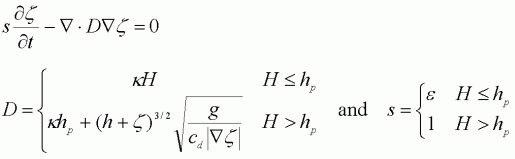
where
hp is the depth of the porous layer that has a porosity of